What Is Not Polynomial? Unmasking the Powerful Class of Functions Beyond Polynomial Bounds

Mathematics thrives on structure—where predictability rules and equations follow strict algebraic rules. Polynomials dominate this landscape, but not everything fits neatly within their rigid framework. What is not polynomial?

This question probes the intricate boundaries of mathematical functions, exposing the rich diversity of expressions that defy polynomial classification. Far from being marginal, non-polynomial functions are foundational in modeling reality’s complexity, from quantum oscillations to chaotic chaotic oscillations in dynamical systems. Understanding what distinguishes non-polynomial functions reveals not only mathematical depth but also their indispensable role across science and engineering.

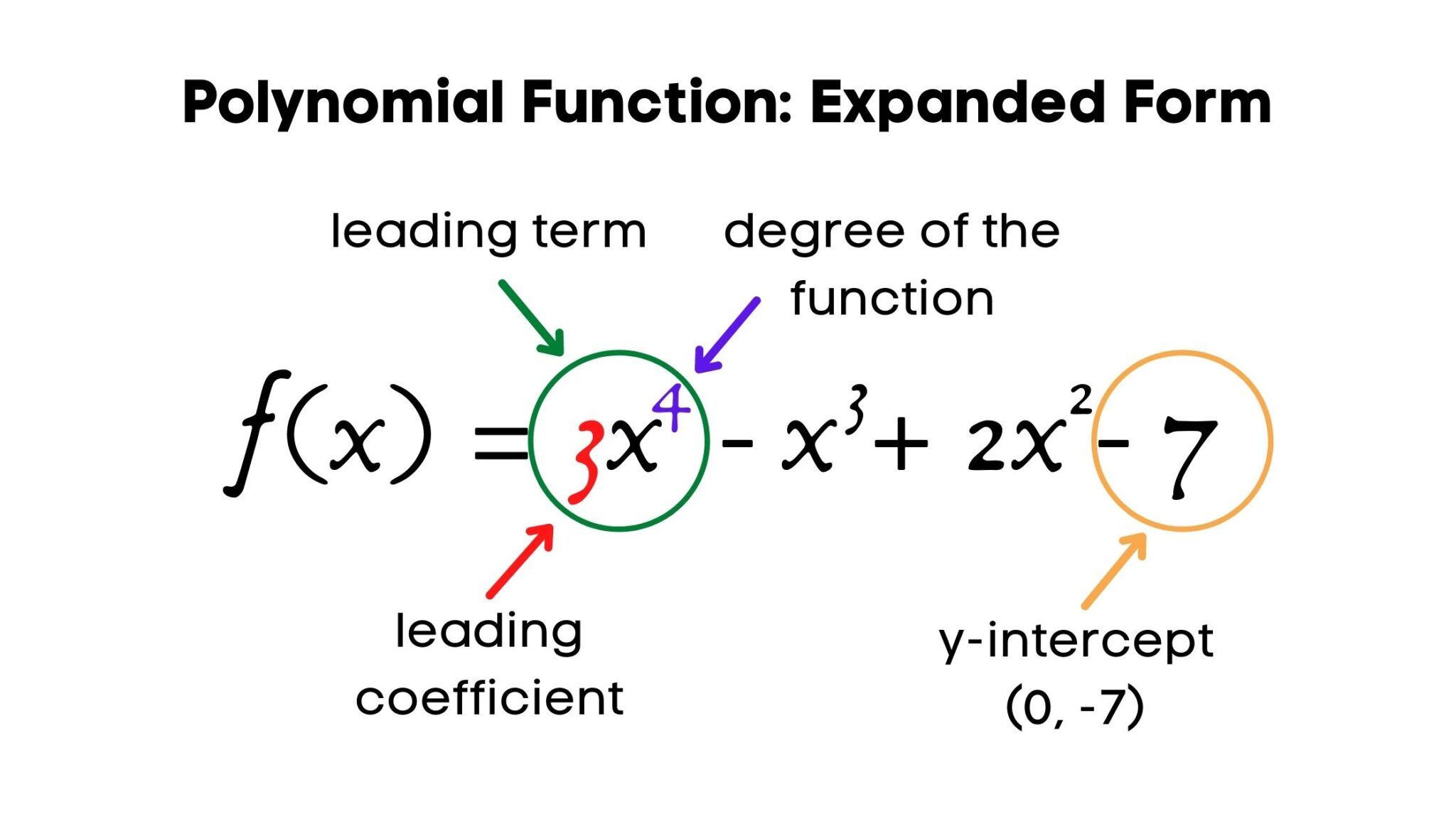
Polynomials are defined by a precise algebraic form: expressions built from variables raised to non-negative integer exponents, combined via addition, subtraction, and multiplication. In contrast, functions that cannot be written as such expressions fall into a vast and varied category often labeled “not polynomial.” What they share is not a single trait, but a rejection of the constrained degree structure and term-based expansion that defines polynomials. “A function is not polynomial if it cannot be expressed as a finite sum of terms like aⁿxⁿ, where n is a non-negative integer,” explains Dr.

Elena Markov, a mathematical analysis expert at MIT. “This includes infinite series, transcendental functions, and expressions involving exponentials, logarithms, and trigonometric evaluations.”

Core Definitions: What Separates Polynomials from the Rest?

The distinction between polynomial and non-polynomial functions lies in several fundamental properties: - **Domain and Continuity**: Polynomials are defined for all real (or complex) values with smooth, continuous behavior—no breaks or vertical asymptotes. Non-polynomial functions often impose restrictions: logarithmic functions have domains limited to positive numbers; rational functions remain undefined where denominators vanish.

- **Degree and Stability**: Polynomials have a clear, finite degree dictating end behavior and growth rates. Non-polynomial functions can grow faster than any polynomial, exhibit oscillations with no clear period, or behave wildly without limiting bounds. - **Closed-Form Expressions**: Polynomials admit closed-form algebraic representations, whereas non-polynomial functions frequently require infinite series or integral forms for accurate modeling.

Consider the exponential function, f(x) = eˣ. This function cannot be written as a finite polynomial; its Taylor series expansion — 1 + x + x²/2! + x³/3!

+ — is infinite, placing it definitively outside polynomial classification. Similarly, trigonometric functions like sin(x) and cos(x) rely on infinite series and transcendental relationships, making them non-polynomial by design and necessity.

Key Examples of Non-Polynomial Functions in Practice

Polynomials set the foundation, but many real-world phenomena demand more expressive tools.

Several major classes of non-polynomial functions play pivotal roles: - **Transcendental Functions** These functions involve transcendental numbers (like e and π) or are defined through limits and infinite processes. - **Exponential Functions**: f(x) = aˣ (a ≠ 0,1) model growth and decay processes in physics, finance, and biology. Their rapid, unbounded growth or decay contrasts sharply with polynomial functions that stabilize as inputs grow.

- **Logarithmic Functions**: f(x) = logₐ(x) capture cumulative effects, such as compound interest or entropy in thermodynamics. Their slow, increasing but bounded-like growth underscores behavior alien to polynomial scaling. - **Trigonometric Functions**: sin(x), cos(x), and tan(x) describe periodic phenomena—from planetary motion to alternating current—exhibiting recurring patterns impossible to encode in polynomial terms without infinite terms.

- **Inverse Functions**: Functions like logₐ(x), √x (the square root), or arcsin(x) reverse polynomial operations but inherently lack polynomial structure due to their non-algebraic nature. Everyday applications—such as modeling radioactive decay, converting sound levels via the decibel scale, or analyzing waveforms—rely on these non-polynomial tools because their behavior defies polynomial simplification.

Why Non-Polynomial Functions Matter: Beyond Algebraic Simplicity

The mathematical world is not exclusively algebraic.

While polynomials offer computational efficiency and structural clarity, non-polynomial functions unlock the ability to describe complex, dynamic, and continuous systems. Their inclusion expands mathematical modeling far beyond static equations into realms of change, continuity, and exponential transformation. These functions enable precise representations of natural laws: - Quantum mechanics uses wavefunctions involving exponential decays and oscillatory trigonometric forms.

- Signal processing depends on Fourier transforms leveraging sine and cosine series. - Financial models incorporate exponential functions for compound interest and risk assessment. - Complex systems like climate dynamics leverage non-polynomial inputs to simulate feedback loops and unsettled equilibria.

As Dr. Markov emphasizes, “Absence of polynomial structure does not mean mathematical obscurity—it means embracing the tools that capture reality’s true complexity.” Without involving exponentials, logs, or trigonometry, mathematical descriptions would collapse under the weight of