Unlocking Trigonometry: Mastering Inverse Functions to Transform Complex Problems
Unlocking Trigonometry: Mastering Inverse Functions to Transform Complex Problems
At the heart of trigonometric mastery lies a powerful set of tools: inverse trigonometric functions. Often overlooked by beginners, these functions unlock pathways through equations that seem unsolvable, transforming abstract relationships into precise real-world applications. From calculating angles in navigation to modeling wave patterns in physics, inverse trig functions serve as bridges between theory and practice.
Unlocking them requires more than memorization—it demands understanding the essence of inverse mapping, domain restrictions, and their geometric significance.
Inverse trigonometric functions—also known as arc functions—reverse the behavior of standard sine, cosine, and tangent functions, returning angles when known ratios are provided. The inverse sine, denoted as arcsin(x), returns an angle in the interval [−π/2, π/2]; similarly, arccos(x) spans [0, π], and arctan(x) outputs values in (−π/2, π/2).
These functions reframe trigonometry from forward relations to inverse problem-solving.
To grasp why inverse functions matter, consider a real-world scenario: a drone flying at a known angle and distance from a receiver. Determining its true bearing directly requires an inverse relation—such as arctangent of latitude over longitude—to extract the correct azimuth. Without inverse functions, such spatial reasoning would collapse into ambiguity.As physicist and educator John R. Whitcomb states, “Inverse trig functions are not just mathematical curiosities—they are essential for translating measured values into directional truths.”
Each inverse trig function is defined over a restricted domain to ensure uniqueness and avoid ambiguity. For example, sine’s primary range [−π/2, π/2] ensures arcsin(x) produces a single, unambiguous angle.
Similarly, arccosine’s domain is confined to [0, π] so that arccos(x) yields a valid angle where cosine equals the input. These constraints reflect the periodic, oscillatory nature of their parent functions—yet within their domains, inverse functions deliver clean, predictable results.
Exploring the Core: Key Inverse Trigonometric Functionsarcsin(x): Bridging Inputs to Sine Angles
arcsin(x), or the arc sine function, answers the question: given a value y between –1 and 1, what angle θ satisfies sin(θ) = y? Defined over [−π/2, π/2], its graph rises monotonically from −π/2 to π/2, reflecting sine’s behavior within this interval.Because sine is bounded and periodic, the restricted domain ensures arcsin(x) gives a single output for every valid input. This function is indispensable in fields like robotics and signal processing, where precise angular calculations from sensor ratios are mission-critical.
Example: Suppose a sonar pulse detects a underwater object at a sine value of 0.5.
To determine the angle of elevation from the receiver, one computes arcsin(0.5) = π/6 (30 degrees). Without the domain restriction, the same sine value could correspond to multiple angles across different rotations—but arcsin minimizes confusion by isolating the principal value.
arccos(x): From Cosine Outputs to Geometric Angles
arccos(x), or the arc cosine, reverses cosine. It answers: for a given x in [−1, 1], what angle θ satisfies cos(θ) = x?Since cosine spans [0, π], the output interval ensures uniqueness. This function plays a central role in physics and engineering, where cosine models forces, light angles, and wave phases. Unlike arcsin, arccos reveals angles directly tied to geometric symmetry—making it vital for construction, optics, and navigation systems.
Real-world impact: When designing satellite dish alignments, engineers use arccos to compute azimuth angles from reflected signal cosine values.
The restricted range prevents incorrect direction assignments, ensuring accurate signal reception.
arctan(x): Mastering Slope Through Angular Input
arctan(x) stands out by mapping slope (rate of rise over run) to angle. Unlike sine and cosine, arctan accepts all real numbers, spanning (−π/2, π/2). This broad domain makes it uniquely suited for analyzing arbitrary inclines, from road gradients to fluid flow velocities.Because tangent spans infinitely with periodic repetition, arctan selects the acute angle, offering clarity where slope alone is ambiguous.
Applications multiply: in computer vision, arctan helps determine object orientation from pixel slope. In financial modeling, arctan transforms normalized returns into directional percent signals, aiding trend forecasting. Its continuous, smooth curve ensures no loss of precision across input extremes.
Understanding domain and range is fundamental.
For arcsin and arccos, inputs must lie within [−1, 1]; for arctan, the full real line supports unrestricted angular output. These constraints prevent erroneous interpretations and preserve mathematical consistency. As fundamental as they are, inverse functions demand careful handling—especially when translating real-world measurements into precise angles.
Practical Applications Across Disciplines
- Engineering & Paley The*> – From robotics to civil design, arctan calculates precise mechanical angles in gear systems and bridge supports.- Physics & Astronomy – arcsin and arccos determine wave interference phases and celestial positions from angle-based observations. - Computer Graphics & AR – inverse tangents convert pixel-to-real-world scaling, enabling immersive augmented reality experiences. - Navigation & Surveying – trigonometric inverses correct sensor data, ensuring accurate GPS positioning and land boundary mapping.
These applications illustrate inverse functions’ role not just in solving equations, but in enabling technological precision and innovation across modern industries.
Approaching Inverses: Strategy and Calculus Insights
Mastering inverse function alignment requires intentional strategy: - Start with known ratios: Whether sine, cosine, or tangent, identifying the output value anchors the inverse process. - Recite principal domains: Knowing arcsin’s [−π/2, π/2], arccos’ [0, π], and arctan’s (−π/2, π/2] sharpens accuracy.- Leverage unit circles: Visualizing reversed sine and cosine relationships maps algebraic inverse steps to geometric intuition. - Validate inputs: Always confirm range restrictions—arccos(−2) and arctan(∞) have no real answer, avoiding undefined outputs. Calculus reinforces understanding: each inverse trig function is defined as the expression limh→0 (arcsin(hx) || arccos(hx) || arctan(hx)), capturing infinitesimal behavior.
This limit perspective confirms their continuity and differentiability within domain boundaries—critical for optimization and numerical methods.
Advanced problem-solving often combines inverse functions with identities and identities or logarithms. For instance, solving arcsin(√3/2) might involve recognizing √3/2 as sin(π/3), but the inverse formalizes and generalizes such shortcuts.
Despite their utility, inverse trig functions present common pitfalls: assuming universal domain across all ranges, misapplying principal values, or neglecting periodicity’s influence.
Clear communication of output intervals and domain awareness prevent miscalculations that ripple through engineering and data science applications.
The Future of Inverse Trigonometry in Technology
As artificial intelligence and machine learning advance, inverse trig functions remain foundational. They power geometric reasoning modules in neural networks, enhance spatial awareness in autonomous systems, and improve signal interpretation in biomedical imaging.The ability to reverse and refine trigonometric mappings underpins deeper learning models capable of nuanced environmental understanding.
In essence, unlocking inverse trigonometric functions is not merely an academic achievement—it is a gateway to precision in a world governed by angles and motion. From the urgency of rescue drone navigation to the subtlety of MRI data enhancement, these functions quietly shape reality.
Mastery demands patience, rigorous application of domain logic, and a deep respect for their mathematical boundaries. But with that mastery comes power: the power to decode complexity, optimize performance, and translate measurement into meaning.


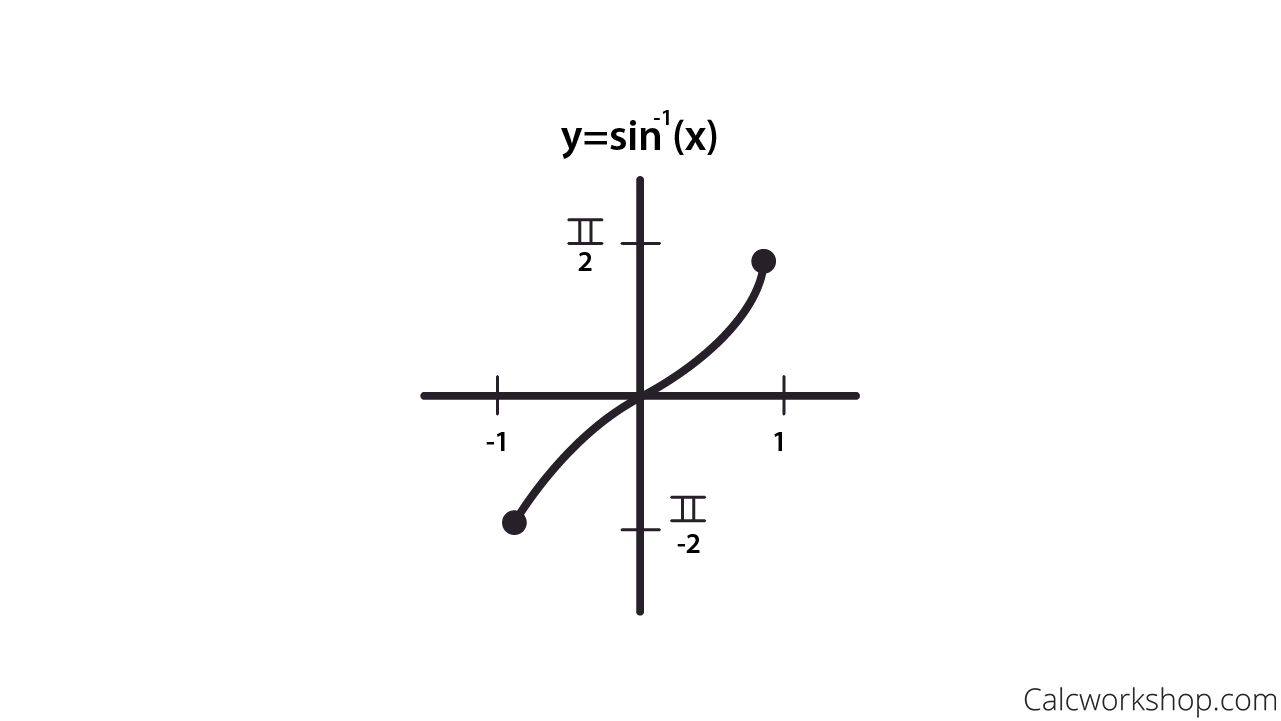

Related Post

The Transformation of Trey Gowdy: From Conservative Firebrand to Strategic Central Figure

At Just 33, He Became the Youngest Pope in History — And Yet Still Changed the Church

How Much Is Justin Trudeau Worth? A Deep Dive Into Canada’s Prime Minister’s Financial Profile

2 Chainz Height The Unveiled Truth: Why the Rap Titan’s Stature Defies Expectations

