Unlocking Trigonometric Precision: How Pythagorean Truths Power Trig Identities
Unlocking Trigonometric Precision: How Pythagorean Truths Power Trig Identities
At the heart of trigonometry lies a deceptively simple geometric relationship—the Pythagorean identity—whose elegant implication reverberates through every corner of trigonometric calculation and application. By asserting that in a right triangle, \( \sin^2\theta + \cos^2\theta = 1 \), this cornerstone identity forms the foundation for transforming complex angular expressions into manageable forms. It is not merely a formula; it is a gateway to simplifying waveforms, modeling oscillations, and solving real-world problems across physics, engineering, and data science.
Understanding its derivation, variations, and widespread use reveals how ancient geometric truths continue to shape modern mathematical reasoning.
The Pythagorean identity arises directly from the Pythagorean Theorem applied to the unit circle. Consider a right triangle inscribed in a unit circle, where one angle θ is measured from the positive x-axis. The adjacent side corresponds to \( \cos\theta \), the opposite side to \( \sin\theta \), and the hypotenuse—the radius—equals 1.
Thus, \( \cos^2\theta + \sin^2\theta = 1^2 \), establishing the identity. This geometric origin underscores its reliability: it merges visual intuition with algebraic power. “This identity is the bridge between geometry and algebra,” notes mathematician Dr.
Elena Vasiliev, “revealing how spatial relationships encode SMOOTH mathematical transformations.”
Core Trig Identities Rooted in the Pythagorean Foundation
The Pythagorean identity serves as the anchor for a family of essential trigonometric relationships. When manipulated through algebraic expansion, it enables the derivation of several powerful identities that define the behavior of sine and cosine across all angles. These include:
- Reciprocal Identities: Dividing both sides by \( \cos^2\theta \) yields \( 1 + \tan^2\theta = \sec^2\theta \); dividing by \( \sin^2\theta \) gives \( 1 + \cot^2\theta = \csc^2\theta \).
These relationships shift focus between ratios, allowing optimization in integral calculus and wave frequency analysis.
- Pythagorean Expressions: Directly from Pythagoras, \( \sin^2\theta + \cos^2\theta = 1 \) remains pivotal for normalizing trigonometric functions and validating identities under transformation.
- Angle Sum and Duality: For angles \( \theta \) and \( \phi \), identities like \( \sin^2(\theta + \phi) = \sin^2\theta + \cos^2\theta \cos^2\phi + 2\sin\theta\cos\theta\sin\phi\cos\phi \) unfold from expansions rooted in Pythagorean geometry, enabling precise angular manipulations.
These derived identities are not theoretical curiosities—they are functional tools. For instance, in electrical engineering, the identity simplifies AC circuit analysis by converting time-varying sine waves into harmonic components expressible through \( \sin^2\theta \) and \( \cos^2\theta \). Similarly, in signal processing, Fourier transforms rely on Pythagorean-based identities to decompose complex signals into orthogonal frequency components.
From Triangles to the Unit Circle: Historical and Geometric Connections
The Pythagorean identity’s roots stretch deep into antiquity, with roots in Euclid’s *Elements*, where geometric proofs establish right triangle relationships that would centuries later anchor trigonometry.
“It began as a shadow of geometry, yet blossomed into a versatile algebraic powerhouse,” muses historian of mathematics Dr. Samuel Rex. “From measuring temple shadows to predicting planetary motion, this identity has enabled clarity where chaos once reigned.”
When extended beyond right triangles to any angle via the unit circle, the identity becomes universally applicable.
At any point on the circle defined by \( (\cos\theta, \sin\theta) \), the sum of squared coordinates equals 1, preserving the Pythagorean truth across infinite radians. This continuity exemplifies the elegance of mathematical invariance—geometric foundations that scale infinitely through rotation, polar coordinates, and complex analysis.
Applications Across Science and Technology
The implications of the Pythagorean identity ripple through numerous scientific disciplines, each leveraging its algebraic structure to decode natural phenomena. In classical physics, the identity underpins energy conservation models in harmonic oscillators, where kinetic and potential energy components combine via trigonometric sums rooted in Pythagorean logic.
Engineers use it to optimize structural vibrations, ensuring buildings withstand resonant frequencies without collapse.
In computer graphics and animation, trigonometric identities derived from the Pythagorean principle animate realistic motion. “Animating a bouncing ball’s elliptical path?
That’s Pythagorean identity in disguise—tracking position, speed, and angle at every frame,” explains computational physicist Lena Cho. “The energy transformation between kinetic and potential forms follows exactly \( \sin^2\theta + \cos^2\theta = 1 \), scaled by damping factors.”
Moreover, statistical modeling benefits through singular value decomposition (SVD), where data covariance matrices—symmetric and positive semi-definite—rely on spectral theory anchored in Pythagorean norms. Principal component analysis (PCA), a cornerstone of machine learning, uses variance maximization instead expressed via trigonometric normalization, preserving geometric meaning across high-dimensional datasets.
Common Pitfalls and Mastery Tips
Although powerful,


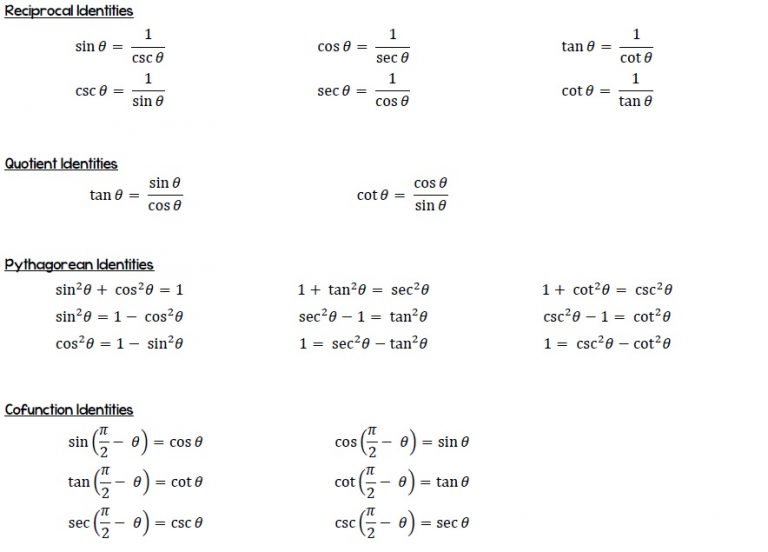
![Trig Identities Derivatives [Inverse, Antiderivative]](https://trigidentities.net/wp-content/uploads/2022/10/Antiderivative-Trig-Identities.jpg)
Related Post

Wyoming Amusement Park: Where Frontier Spirit Meets Thrill on the High Plains

The Revolutionary Economics of Human Agency: How Depay Redefines Value and Agency in Modern Markets

Amalia Williamson Age: The Rising Star Reshaping Scottish Heritage in the Digital Age

What Is The Purpose Of This Cellular Process? Unlocking Life’s Master Blueprint

