Unleashing the Power of Sin, Cos, and Tan: How These Trigonometric Forces Shape Modern Science and Technology

In a world governed by precision and pattern, trigonometric identities—particularly sine (sin), cosine (cos), and tangent (tan)—serve as the mathematical bedrock underlying everything from digital imaging and medical diagnostics to satellite navigation and artificial intelligence. These interrelated functions not only define the geometry of waves and circles but also power the algorithms driving modern innovation. Without sin, cos, and tan, the digital age as we know it—reliant on signal processing, motion modeling, and 3D rendering—would collapse under its own complexity.

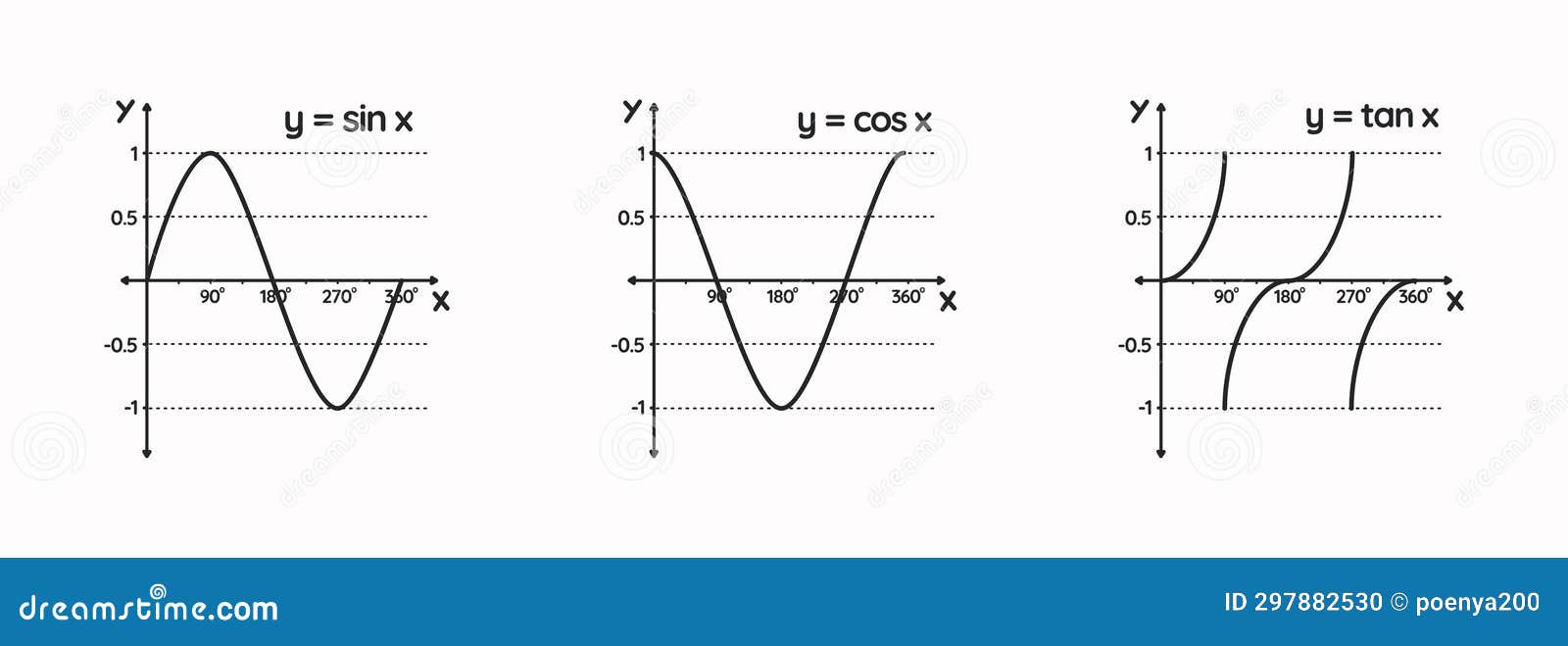
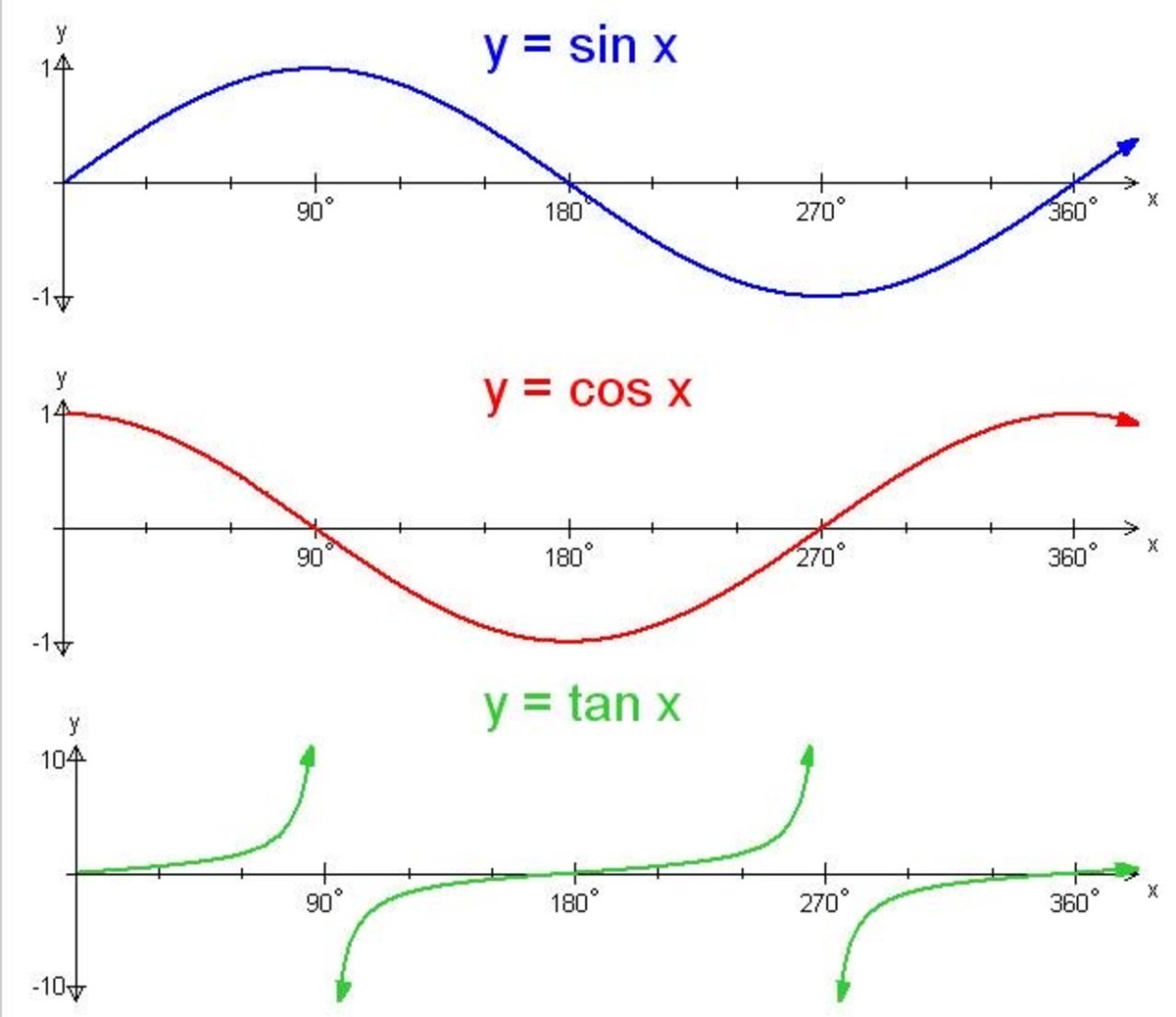
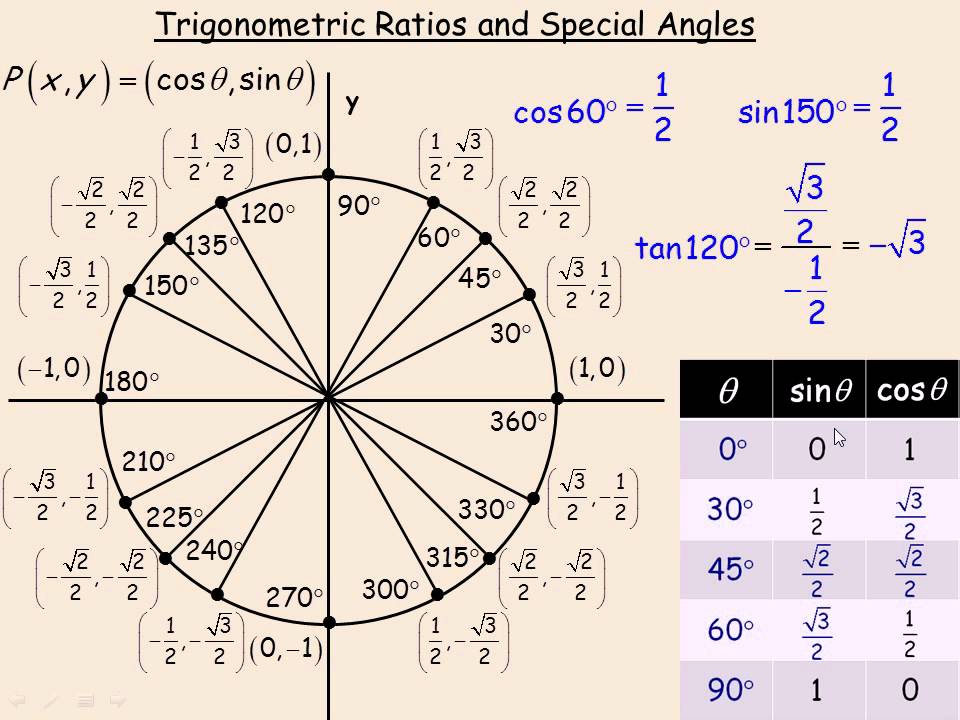
At their core, sine, cosine, and tangent are the ratios of sides in a right triangle, embedded deeply in calculus, physics, and engineering. Defined on the unit circle, where the hypotenuse measures 1, sin(θ) represents the vertical coordinate, cos(θ) the horizontal, and tan(θ) = sin(θ)/cos(θ) the slope of the line making angle θ with the axis. These definitions transcend basic geometry, becoming indispensable tools for analyzing periodic phenomena, rotational dynamics, and spatial transformations.

Sine and cosine form the foundation of periodic motion. Any recurring wave—be it sound, light, or electrical current—can be expressed as a sum of sine or cosine functions, a principle formalized in Fourier analysis. This decomposition into harmonic components enables engineers to filter noise, compress data, and decode signals with remarkable fidelity.

"Fourier transforms, built on sine and cosine, are the silent architects of digital audio and wireless communications," explains Dr. Elena Marquez, a signal processing expert at MIT. "They allow us to reverse-engineer history—from recovering historic audio recordings to decoding Wi-Fi signals.” The phase shift and amplitude modulation enabled by these functions are not just theoretical—they’re tangible forces shaping how we hear, see, and connect across distances.

The Dynamic Duo: Sinusoidal Data in Real Time

Beyond steady waves, sin, cos, and tan govern dynamic, rotating systems. Cosine functions, with their natural zero-crossing at 90°, model oscillatory processes with phase shifts. For instance, in electric power systems, alternating current (AC) voltage follows a sinusoidal waveform: V(t) = V₀·sin(ωt), where ω represents angular frequency.

Near-real-time monitoring of such signals depends on precise measurement of sin and cos values across time—enabling grid stability, energy efficiency, and fault detection. Rotation, Rotation, Repeat Trigonometric ratios are indispensable in describing rotation. The coordinates of a point on the unit circle are (cosθ, sinθ), turning abstract angles into spatial coordinates.

This principle extends to robotics, where joint angles are converted into physical movement. A robotic arm’s endpoint position, for example, is calculated via cosine and sine of its pivot angles. Similarly, GPS relies on orbital mechanics grounded in sinusoidal functions.

Satellites orbit Earth along elliptical paths modeled by differential equations solved using sin and cos. Without these functions, precise positioning—critical for self-driving cars, drone navigation, and global logistics—would remain beyond reach.

Beyond Geometry: tan and the Slope of Innovation

The tangent function plays a hidden yet critical role in determining rates of change—cornerstones of calculus and optimization.

Tangent’s asymptotic behavior near odd multiples of 90° reveals critical thresholds in systems modeling growth or decay. In machine learning, gradient descent algorithms rely on computing derivatives—frequently involving tan(θ)—to adjust model parameters efficiently.