The Precise Power of Base In Mathematics: Foundation of Number Systems and Their Real-World Impact
The Precise Power of Base In Mathematics: Foundation of Number Systems and Their Real-World Impact
Base In mathematics is not merely a technical detail but the invisible architecture underlying all number representations—from ancient abacuses to modern computing. At its core, a base defines how digits encode quantity within a positional numeral system. This fundamental concept governs how we count, compute, and translate information across domains, shaping everything from digital electronics to cryptography.
Mastery of base systems reveals the silent logic that makes digital precision and human numeral interpretation possible.
Defining Base In Mathematics: A Foundational Concept
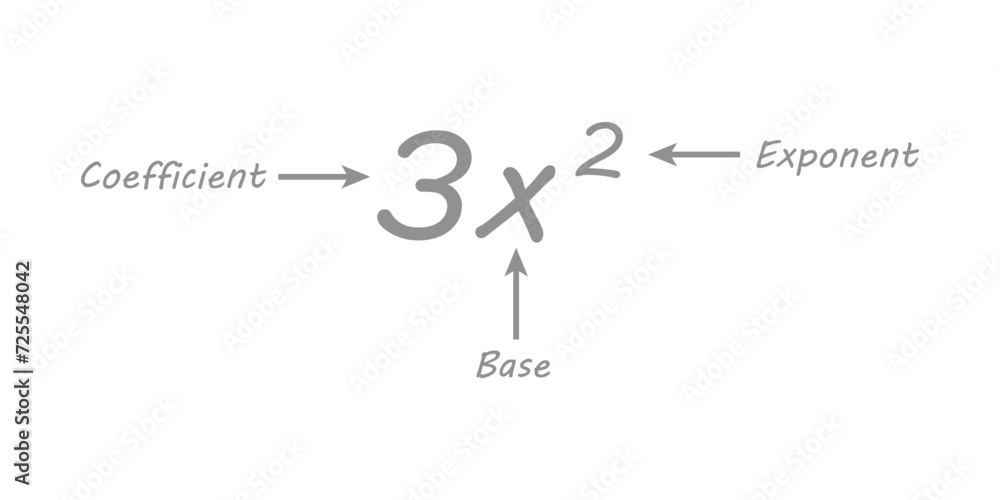
Base In mathematics refers to the numerical system in which every digit represents a power of a chosen base, typically greater than one. Formally, a base-b numeral system uses digits 0 through b−1, with place values determined by increasing powers of b. For example, in base 10—the system universally used today—the number 345 means: 3 × 10² + 4 × 10¹ + 5 × 10⁰
This positional notation allows efficient representation of large values using only small symbols.
Unlike unary or binary systems (base 2), base b balances expressiveness and complexity, enabling compact encoding of quantities across scales.
Formally, any whole number N in base b can be expressed as a sum: N = dₙ × bⁿ + dₙ₋₁ × bⁿ⁻¹ + … + d₁ × b¹ + d₀ × b⁰, where each digit dᵢ satisfies 0 ≤ dᵢ < b. This definition unifies cultures, industries, and technologies under a single mathematical language.
The Historical Evolution of Positional Bases
The origins of base systems trace back thousands of years, with evidence of base 60 (sexagesimal) use by Sumerians and Babylonians around 1800 BCE. Their choice of base 60 persists today in timekeeping (60 seconds, 60 minutes) and angular measurement (360 degrees), due to its high divisibility.
Yet base 10 emerged as dominant globally, likely because human anatomy—ten fingers—provided an intuitive counting basis.
Islamic scholars, particularly Al-Khwarizmi, advanced the conceptualization of positional notation in the 9th century, formalizing the use of zero as a placeholder—a breakthrough that enabled precise arithmetic and algebra. By the Renaissance, European adoption of the Hindu-Arabic numeral system cemented base 10 as the standard for commerce and science.
Modern Computing and the Exclusive Role of Base 2
In digital electronics, base 2 underpins the very logic of computation. Computers process data using binary states—on (1) and off (0)—making base 2 the natural language of circuits and processors.
All digital signals, memory addressing, and instruction sets derive from binary arithmetic.
Transitioning beyond binary, engineers utilize higher bases for efficiency. Base 16 (hexadecimal), with digits 0–9 and A–F, compresses 4 binary digits into a single symbol, streamlining programming and memory debugging.
Similarly, base 2³⁴ underpins modern computing architectures, allowing compact representation of large addresses and cryptographic keys.
Beyond Base 10: Academic and Scientific Applications
While base 10 dominates human-centric mathematics, other bases serve specialized academic and scientific roles. The portbases ing 2 offer clear parity in error checking and optical encoders; base 12, with its rich divisibility (factors 2, 3, 4, 6), is championed in specialized metrology and retail systems; base 8 (octal) historically served as a concise shorth



Related Post

The Jungle Book 2016 Cast: Revolutionizing Animal Voices with Timeless Sound

Eva Mendes at 38: The Veteran Actress Whose Age Defines Her Timeless Career

Roadrunner en Español: La Guía Definitiva para una Traducción Clara y Efectiva

Mastering Acid-Base Chemistry: Balancing Title-Reversing Neutralization Reactions That Define Industrial and Environmental Processes

