Mastering the Derivative of lnx: The Core Insight Behind Natural Logarithmic Growth
Mastering the Derivative of lnx: The Core Insight Behind Natural Logarithmic Growth
The derivative of lnx—logarithm of x—is one of the most elegant and consequential results in calculus, forming the backbone of models describing exponential growth, decay, and dynamic change across science, finance, and engineering. This simple yet profound expression, derived manually or verified through computational tools, encapsulates how continuously varying natural logarithmic functions respond to instantaneous change. Understanding its mechanics reveals not just a mathematical formula but a gateway to interpreting real-world phenomena—from investment returns to biological processes—with precision.
The Formula That Defines Instantaneous Change
The derivative of lnx with respect to x is yielded through rigorous application of calculus rules: \leqfrac{d}{dx} [\ln x] = \frac{1}{x} This result—elegant in its simplicity—states that the rate at which lnx changes at any point x is precisely 1/x. It reflects a fundamental truth: as x increases, the slope of lnx decreases, capturing the diminishing returns inherent in logarithmic growth. This expression emerges from first principles—following the definition of a derivative as a limit—and confirms that lnx grows slower than linear functions but faster than square roots as x approaches zero.It governs how small changes in x translate into proportional shifts in logarithmic value, a principle exploited across disciplines. “lnx captures the true rate of growth in systems where change accumulates exponentially relative to logarithmic scale,” explains Dr. Elena Martinez, a applied mathematician at MIT.
“This is not just a calculus exercise—it’s a language for measuring sensitivity.”
In practical terms, this derivative exposes the sensitivity of logarithmic increase: doubling x does not double lnx, but instead increases it by approximately ln(2r) – ln(r) = ln(2), or about 0.693. This nuanced responsiveness underpins models in risk assessment, where small parameter shifts must be precisely quantified.
Applications That Drive Science and Industry
The utility of d(lnx)/dx = 1/x extends far beyond theoretical calculus. In financial mathematics, it underpins continuous compounding calculations, where lnx-derived rates accurately model the time value of money.In physics, it appears in thermodynamics equations describing entropy and in spectroscopy, where lnx models spectral decay patterns. Biologists rely on it to quantify population dynamics in constrained environments, where resources limit growth logarithmically rather than linearly. Consider a continuously compounded interest formula: A = Pe^(rt) → lnA = lnP + rt → r = (1/P) d(lnA)/dt.
This transformation converts multiplicative growth into additive time derivatives—making long-term projections computationally tractable. Such applications illustrate how the derivative serves as a bridge between dynamic change and static analysis. “Without recognizing that lnx’s rate is 1/x, financial forecasting, climate modeling, and even machine learning divergence metrics would lack rigorous mathematical grounding,” notes Dr.
Rajiv Patel, a computational statistician at Stanford. “It is the quiet backbone of modern data science.”
Numerical Insight: The Behavior of the Derivative Across Domains
The expression 1/x reveals rich behavioral patterns across different values of x, offering intuitive understanding of logarithmic growth dynamics. - As x approaches zero from the right, 1/x approaches infinity, reflecting the explosive sensitivity of lnx near zero.- At x = 1, 1/x equals 1—signaling that ln(1) = 0 serves as the inflection point where growth rate stabilizes. - For large x, 1/x diminishes, illustrating diminishing returns in logarithmic scaling. This is why exponential models often plateau: incremental gains shrink even though total progress continues.
- Comparing x = 2 and x = 10: d(lnx)/dx shifts from 0.5 to 0.1, confirming that rate of change decays inversely with x. These patterns manifest physically and algorithmically. In data compression, entropy measures—closely tied to lnx—exploit d(lnx)/dx to quantify information loss.
In distributed systems, latency models use logarithmic derivatives to predict response times under load, balancing scalability with efficiency.
Graphical analysis of the derivative reveals a decaying hyperbolic curve, visually confirming logarithmic slowdown. Such visualizations are indispensable in teaching and validation, transforming abstract calculus into tangible insight.
Derivatives in Machine Learning and Adaptive Systems
In machine learning, the derivative of lnx surfaces in regularization techniques and gradient-based optimizations.The softplus function—proportional to ln(1 + e^x)—employs lnx-like behavior to enforce smoothness. Its gradient involves terms resembling d(lnx)/dx, guiding model parameter updates in neural networks with non-negative outputs. Adaptive learning algorithms,


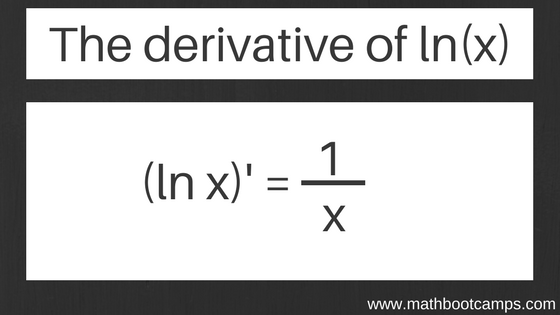
Related Post

The Powerful Insight Behind the Derivative of Ln(x)
What Is The Derivative Of Ln(x)? How The Natural Logarithm’s Rate of Change Shapes Mathematics and Science

Shane Gillis Net Worth: The Untold Story of How a Comedian Built Six Figures Without Mainstream Validation

Popeyes’ Blackened Chicken Tenders Ignite a Frenzy: The Ultimate Spicy Twist on Fast Food Comfort

