How Fick’s Second Law Governs the Invisible Dance of Molecular Diffusion in Science and Industry

The invisible choreography of molecules moving from patent to perfumed space unfolds through a fundamental physical principle: Fick’s Second Law. This scientific cornerstone describes how concentration gradients drive the diffusion of particles, shaping processes from drug delivery to environmental remediation. As technology advances, understanding this law is no longer academic—it is operational, enabling engineers and biologists to predict, control, and harness molecular transport with precision.

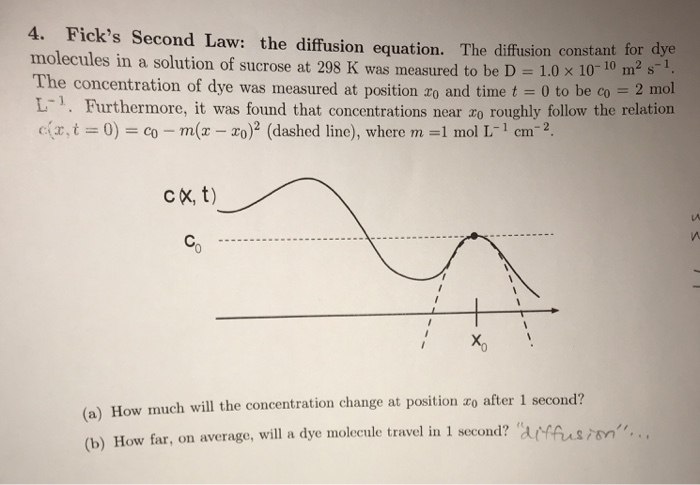
At its core, Fick’s Second Law reveals not just movement, but the dynamic balance between order and randomness in nature. Fick’s Second Law, derived mathematically from diffusion dynamics, expresses the rate of change in concentration over time relative to spatial gradients. In its differential form, ∂C/∂t = D ∂²C/∂x², it states that the second spatial derivative of concentration (dC/dx²) multiplied by the diffusion constant (D) determines how rapidly a substance spreads.

This formulation captures the essence of spontaneous dispersion—why perfume lingers in a room, why a saline solution slowly saturates tissue, and how pollutants migrate through soil. The law emphasizes that diffusion is not uniform; it accelerates as gradients steepen, but asymptotes to equilibrium, governed by material properties.

Central to this understanding is the diffusion coefficient, D—a parameter sensitive to temperature, medium viscosity, and molecular mass.

In water at 25°C, for instance, D ≈ 10⁻⁹ m²/s, indicating how sluggish gas replacement is in aqueous environments. In air, D is roughly 2×10⁻⁵ m²/s—orders of magnitude larger—explaining why odors diffuse quickly across open spaces. Temperature plays a pivotal role: increasing thermal energy enhances molecular motion, amplifying D and thus the speed of diffusion.

This temperature dependence is well-validated by experimental data from material science, showing up to a 30% increase in D for polymers when heated.

Real-world applications illuminate Fick’s Second Law’s predictive power. In pharmaceutical engineering, it guides the design of controlled-release capsules.

By modeling D and diffusion distance, researchers engineer coatings that regulate how quickly a drug dissolves, ensuring steady plasma levels over days or weeks. Advanced simulations incorporating the law now enable virtual prototyping, reducing costly trial-and-error in drug formulation. Similarly, environmental engineers rely on the law to map contaminant plumes in groundwater.

Understanding the interplay between hydraulic gradients and subsurface diffusion allows for precise modeling of toxin dispersion, improving remediation strategies.

“Diffusion is not just a passive drift—it’s a controlled process when we apply Fick’s Second Law,” explains Dr. Lena Petrova, a diffusion physicist at the University of Oslo.

“The law quantifies how far and how fast molecules penetrate barriers, enabling us to design smarter materials and intervention protocols.” This precision is critical in emerging fields such as targeted drug delivery, where liposomes or nanoparticles must navigate complex biological landscapes to reach specific cells. By shaping diffusion pathways through engineered microenvironments—adjusting surface charge, size, or porosity—scientists exploit the law to delay or accelerate release kinetics with remarkable accuracy.

The law’s reach extends beyond biology and medicine.

In semiconductor fabrication, dopant atoms diffuse into silicon substrates to create p-n junctions—the heart of electronic devices. Process control hinges on modeling D under varying annealing temperatures, ensuring uniform, reproducible performance. Catalyst design also leverages diffusion principles: porous catalyst supports maximize surface area, but only if active sites remain accessible via efficient molecular transport described by Fick’s Second Law.

Even in food science, moisture migration during storage depends on diffusion gradients; understanding this prevents staleness by predicting how water shifts between ingredients.

At its heart, Fick’s Second Law exposes the deterministic yet stochastic nature of molecular motion. Innovations in computational modeling now integrate real-time data from sensors, enhancing predictive reliability.

Machine learning algorithms, trained on high-resolution diffusion experiments, refine D estimates and boundary conditions, pushing the boundaries of what can be modeled. This synergy between classical physics and modern analytics promises breakthroughs in nanomedicine, renewable energy storage, and climate adaptation technologies.

Fick’s Second Law endures as a silent architect of invisible processes—governing how substances traverse boundaries in ways once hidden to the naked eye.

Its principles form the backbone of diffusion-driven technologies shaping modern life. From healing through timed-release therapies to securing safe water and clean energy, the law transforms the unpredictable dance of molecules into measurable, controllable order. As science and engineering evolve, so too does our mastery of this foundational truth—reminding us that even the smallest moves are governed by powerful, predictable laws.

The Core Equation: A Mathematical Window into Molecular Flow

At the heart of Fick’s Second Law lies a deceptively simple yet profoundly insightful equation: ∂C/∂t = D ∂²C/∂x² This formula captures the delicate balance between time evolution (left side) and spatial diffusion (right side). The second derivative ∂²C/∂x² quantifies how sharply concentration changes with position—steeper gradients drive faster diffusion. Multiplying by D, the diffusion constant, sets the rate: high D speeds molecular spread, low D restricts it.

The product defines the pulse of change, translating microscopic randomness into macroscopic predictability.

The elegance of this equation lies in its universality. It applies whether molecules traverse cellular membranes, pollutants seep through soil, or vapor molecules navigate industrial chambers.

Diverging media, altered temperatures, or complex geometries require adaptation—extensions of the law incorporate harmonic coordinates, non-Fickian behavior, or multi-scale modeling—but the foundational insight remains intact. The law’s predictive power empowers engineers and researchers to simulate scenarios that are otherwise