How Do You Calculate A Residual? The Key to Unlocking Model Accuracy

< Rendered with precision, residuals hold the latent clues to understanding how well statistical models perform, serving as the difference between prediction and reality. In fields ranging from economics to machine learning, the residual—the discrepancy between observed value and model-predicted output—offers a clear diagnostic of model strength. But calculating residuals is more than a mechanical step; it is an essential act of validation that transforms abstract equations into actionable insight.

Mastering residual calculation allows analysts and researchers to detect systematic errors, refine models, and ultimately make more accurate, reliable forecasts.

At its core, a residual measures the “leftovers” after a model has done its best to explain data patterns. Formally defined, the residual for a data point is the observed value minus the predicted value.

This simple yet powerful formula—residual = observed − predicted—forms the foundation of model evaluation across disciplines. Whether analyzing housing prices, stock trends, or patient outcomes, residuals reveal which predictions align with reality and which fall short.

The Residual Formula: A Precise Measurement of Prediction Error

< Residual calculation follows a rigorous mathematical rule: each observation contributes one residual, defined as he difference between actual outcome (y_i) and the model’s forecasted value (ŷ_i). The formula is straightforward: residual_i = y_i − ŷ_i This subtraction captures how much the model missed.

A positive residual indicates underestimation; a negative residual signals overprediction. For example, if a model forecasts $250,000 for a home’s sale price, but the actual sale was $275,000, the residual is $275,000 − $250,000 = $25,000. This $25,000 deviation quantifies the model’s failure in this specific instance.

While the elementary equation is concise, real-world applications often reveal layered complexity.

Residuals must be assessed across the entire dataset, not just in isolation. A model may appear broadly accurate yet systematically miscount residential prices upward in one district while underpredicting art collections in another.

Residual Analysis: Diagnosing Model Strengths and Weaknesses

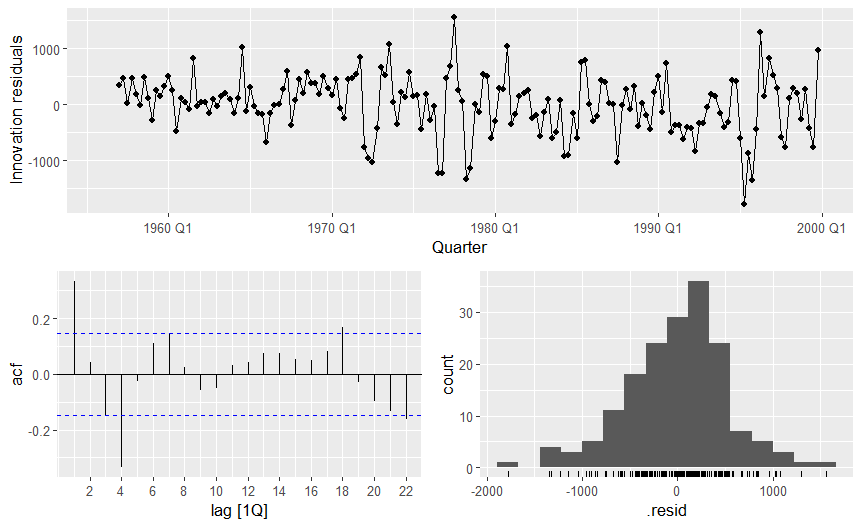
< Beyond mere calculation lies the vital practice of residual analysis—a systematic review of residuals to detect patterns not explained by the model. A well-constructed residual plot—typically residuals plotted against predicted values—crowds crucial diagnostic information.

Key indicators in such visualizations include: - **Random scatter around zero**: A strong sign of a reliable model with no apparent bias. - **Patterns or trends (e.g., upward/downward slopes)**: Suggests model misspecification, such as omitted variables or incorrect functional form. - **Heteroscedasticity** (increasing variance with predicted values): Signals the model’s sensitivity to data scale, undermining consistent accuracy.

These cues transform numbers into narrative—guiding analysts toward necessary model adjustments.

Types of Residuals: Raw, Standardized, and Studentized Values

< Traditional residuals, though informative, carry the original scale of measurement, which may obscure subtle issues when data spans orders of magnitude. To address this, statisticians employ refined residual types: - **Raw residuals**: Direct differences (y − ŷ), easiest to interpret but scale-dependent. - **Standardized residuals**: Residuals divided by their estimated standard deviation.

This normalization to a mean of zero and standard deviation of one enables cross-variable comparison. - **Studentized (or student residuals)**: Residuals adjusted for leverage—how much influence each data point has on model estimates. These reduce high-leverage points’ distortion, offering a cleaner diagnostic for outliers.

Adopting these forms strengthens diagnostic precision, making residual analysis both scalable and context-aware.

Multiple Residual Metrics: Acquiring a Holistic View of Model Performance

< Residuals by themselves convey point-level error but fail to capture overall model fit. To supplement, researchers compute aggregated metrics derived from residuals: - **Residual Sum of Squares (RSS)**: The sum of squared residuals, minimizing total prediction error and anchoring models in least-squares principles. - **Root Mean Squared Error (RMSE)**: The square root of